10.5.2 Составные квадратурные формулы
Существует иной альтернативный подход для повышения точности численного интегрирования.
Разобьем отрезок [a, b] на N частей и обозначим их как 
. Тогда
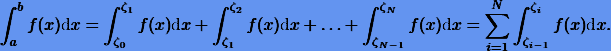
Применяя какую-либо из формул численного интегрирования к каждому интегралу в правой части, получим составную квадратурную формулу для исходного интеграла. Например, применяя формулу трапеций, будем иметь составную квадратурную формулу
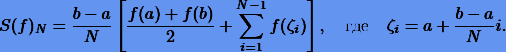
Нетрудно также получить составную формулу Симпсона. Ее можно представить в виде
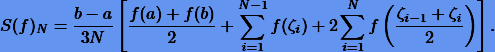
Оценим ошибку составной формулы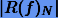 
с разбиением N. Согласно (10.10) имеем
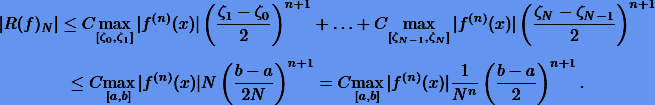
Сравнивая эту оценку с (10.10), можно полагать, что ошибка составной формулы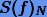 
будет меньше ошибки исходной квадратуры S(f), причем с увеличением N точность составной квадратуры должна повышаться.