ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

11.1 Разложение в ряд Тейлора

Одним из старейших методов решения дифференциальных уравнений является метод разложения в ряд Тейлора.

Найдем решение уравнения (11.1)

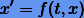
для заданного значения 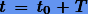при начальном условии . Потребуем, чтобы ƒ была аналитична в точке 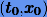. Дифференцируя уравнение по t, будем иметь

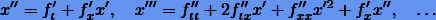
Подставляя t₀ и x₀, последовательно получаем

Таким образом, при достаточно малом Т приближенное решение в окрестности t₀ можно представить в виде ряда Тейлора

Оборвем (усечем) ряд (11.4) нар-ом члене. Тогда получим приближенную формулу р-порядка

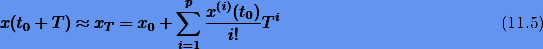
с погрешностью

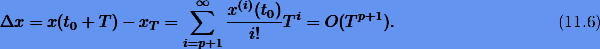
Нетрудно видеть, что при малых Т погрешность Δx (ошибка усечения) будет определяться, главным образом, первым членом ряда (11.6)

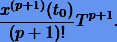
Его называют главным членом погрешности.

Если для 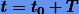ряд Тейлора (11.4) расходится или ошибка приближенной формулы (11.5) довольно большая, то прибегают к так называемому пошаговому интегрированию. Разбивают 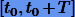на малые отрезки 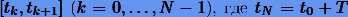, и последовательно получают приближенные решения по формуле

где 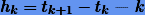-ый шаг интегрирования.

Рассмотрим частные случаи. Для p = 1 и p = 2 с постоянным шагом h имеем формулы

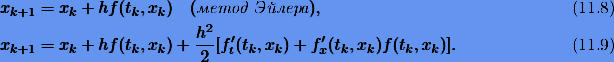
Главным недостатком метода разложения в ряд Тейлора является то, что для получения производных (11.3) необходимо знать производные от f как функции t и x. Очевидно, если f — сложная функция, получение этих производных может представлять собой весьма утомительное занятие. В связи с этим методы разложения в ряд Тейлора редко используются на практике.