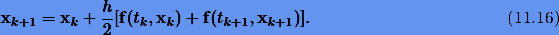ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

11.2 Методы Рунге-Кутты

В начале прошлого века Рунге, а затем Хойн и Кутта предложили подход, основанный на построении приближенной формулы близкой к (11.5), не содержащей производных от f. Методы Рунге-Кутты второго порядка имеют общий вид

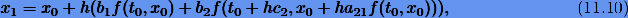
или

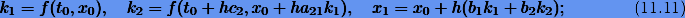
где 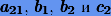— постоянные, подлежащие определению.

Определим постоянные схемы интегрирования так, чтобы она имела второй порядок. Разложим (11.10) в ряд:

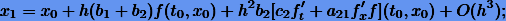
и сравним с разложением точного решения:

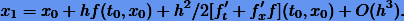
Следовательно, чтобы схема интегрирования имела второй порядок постоянные должны удовлетворять уравнениям

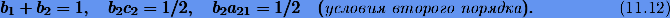
Система уравнений (11.12) дает однопараметрическое семейство решений, которое можно представить в виде

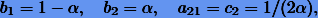
где - свободный параметр.

Например, при имеем формулу Хойна

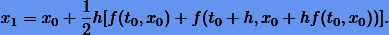
Рунге продемонстрировал идею получения методов интегрирования только для низких порядков. Но именно Кутта сформулировал общую схему того, что теперь называется методами Рунге-Кутты.

Дадим определение этих методов применительно к векторной задаче Коши

Метод

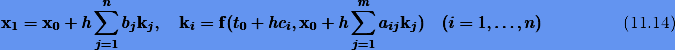
называется n-этапным (n-стадийным) методом Рунге-Кутты для задачи Коши (11.13). Если , то метод явный и каждый следующий коэффициент k_i выражается по предыдущим; если 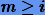, метод неявный и коэффициенты находятся из нелинейных уравнений итерационным способом.

Очевидно, метод Эйлера (11.8) является частным случаем методов Рунге-Кутты, а именно это — явный одноэтапный метод Рунге-Кутты первого порядка. На практике широко применяется явный 4-этапный классический метод Рунге-Кутты 4-порядка

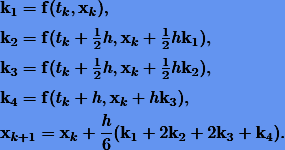
Простые примеры неявных методов Рунге-Кутты — это неявный метод Эйлера (первого порядка)

и метод трапеций (второго порядка)