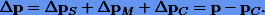1 Основы теории погрешностей

1.1 Численное моделирование и возникновение погрешностей

Одним из методов познания явления (процесса или объекта) является математическое моделирование. Математическая модель представляет собой совокупность уравнений (соотношений), связывающих между собой параметры, которые непосредственно характеризуют состояние исследуемого явления. Таким образом, исследовательский процесс сводится к решению конкретной математической задачи, а именно к решению соответствующих уравнений.

В последнее время главным образом за счет интенсивного развития компьютерных технологий для изучения моделей все чаще прибегают к численным методам. Процесс разрешения математической модели численным методом на компьютере называется численным моделированием (рис. 1.1).

Очевидно, численное моделирование сопряжено с численными ошибками (погрешностями), которые обусловлены: 1) неточностью представления связей между параметрами в математической модели и ошибками исходных параметров; 2) неточностью численного метода; 3) ошибками округления в компьютерной арифметике. Рассмотрим их на примере численного моделирования орбитального движения (рис. 1.1).

Движение объекта на орбите определяется непрерывным изменением его вектора положения р. Учитывая основные факторы, действующие на объект, движение можно формализовать в виде дифференциальных уравнений относительно р вместе с исходными данными р₀ на некоторый момент времени t₀, что составляет математическую модель орбиты p_S. Дифференциальные уравнения не точно представляют движение, а их начальные данные содержат ошибки. Это влечет неустранимую ошибку модели Δp_S = р - p_S (1). Для получения координат из дифференциальных уравнений используют какой-либо приближенный метод численного интегрирования, который, в свою очередь, вносит дополнительные искажения в описании орбитального движения Δp_M = p_S - p_M (2), где p_M — результат интегрирования уравнений. Поскольку все вычисления в компьютерной арифметике выполняются с некоторой точностью, конечный результат численного моделирования p_C будет также содержать в себе вычислительную ошибку Δp_C = p_M - p_C (3). Таким образом, полная погрешность численной модели будет состоять из трех погрешностей: