1.3 Запись чисел на компьютере
Величина вычислительной погрешности главным образом зависит от способа представления числа на компьютере. В современных компьютерах вещественные числа представляются в так называемой форме с плавающей точкой:
где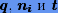 
— целые положительные числа: 
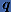— основание системы счисления; 
— цифры числа х в пределах 
— число разрядов. Целое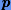 
— порядок числа х, причем 
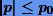. Как нетрудно заметить, значение суммы (или так называемой мантиссы) в (1.3) должно находиться на полуотрезке 
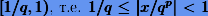. Например, представление числа с двойной точностью в двоичной системе счисления предполагает, что 
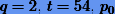= 1024.
Между тем во многих дешевых калькуляторах используется более простая форма представления числа, а именно с фиксированной точкой, где в отличие от (1.3) порядок числа фиксирован: 
.
Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева. Таким образом, числа с двойной точностью в двоичной системе счисления будут иметь 54 значащие цифры. В десятичной системе счисления числа с двойной точностью представляются 16 значащими цифрами. Значащую цифру называют верной, если погрешность числа по величине не превосходит половины единицы разряда, соответствующего этой цифре. Например, число 3.14 представляет число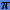 
с точностью до трех значащих цифр (т.е. только три цифры верные), поскольку величина погрешности не превышает 0.005. Отсюда погрешность числа, представленного в форме (1.3), (ошибка округления) при всех верных цифрах не должна превышать
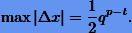
Важной характеристикой точности компьютерной арифметики является число 
, называемое машинным эпсилон. Эта характеристика определяется как расстояние между единицей и ближайшим к ней числом в системе машинных чисел. Так в качестве машинного эпсилон можно выбрать число
