2.1 Метод дихотомии
Положим, что на отрезке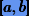 
находится один корень, который необходимо найти с точностью до величины 
Очевидно, что 
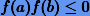. Тогда для поиска решения уравнения (2.1) можно прибегнуть к так называемому методу дихотомии.
Метод дихотомии (или деления отрезка пополам) состоит в следующем (Рис. 2.1).
1. Определяем середину отрезка
.
2. Если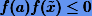 
(корень на 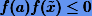), то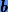 
присваиваем 
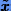; иначе (корень на 
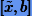) a присваиваем .
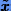3. Если величина отрезка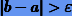 
, возвращаемся к этапу 1; иначе заканчиваем процесс.
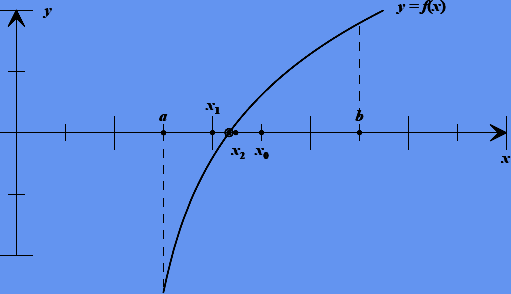
Рисунок 2.1 — Метод дихотомии
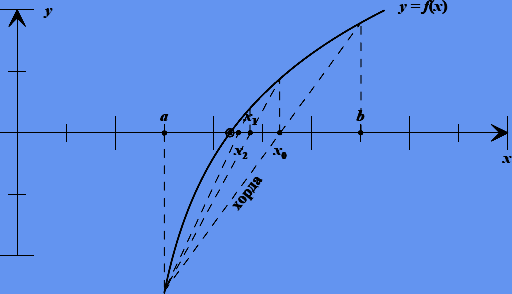
Рисунок 2.2 — Метод хорд
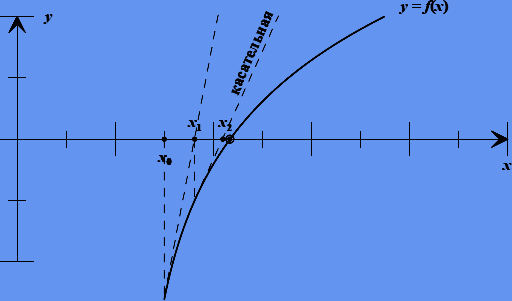
Рисунок 2.3 — Метод касательных (Ньютона)