2.2 Метод хорд
В методе хорд в качестве приближенной оценки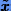 
выбирается не середина отрезка 
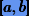, а его пересечение с хордой, имеющей координаты 
(Рис. 2.2). Очевидно, эта оценка будет точнее представлять решение уравнения (2.1), нежели середина отрезка, а потому и алгоритм метода будет выполняться быстрее. В частности, для линейной функции ƒ(x) метод хорд будет давать точное решение.
Алгоритм метода хорд такой же, как и в методе дихотомии с той лишь разницей, что оценка 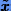вычисляется по одной из формул
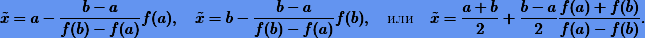
Кроме того, заметим, что в методе хорд используется другой критерий завершения вычислительного процесса: последовательные приближения 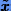вычисляются до тех пор, пока разность текущего и предыдущего приближений по величине не станет меньше задаваемой величины 