2.4 Метод секущих
Если взятие производной в (2.3) проблематично, то ее можно заменить конечной разностью
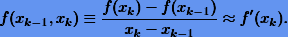
В итоге, итерационная схема (2.3) перепишется как
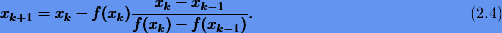
Важно заметить, что для использования схемы (2.4) необходимы две начальные оценки x0 и x1. Обычно это достаточно близкие величины, однако в то же время их выбор не должен допускать обращения разности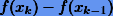 
в машинный нуль.
Метод, основанный на схеме (2.4), называется методом секущих (Рис. 2.4), поскольку каждое новое приближение xk+1 есть корень секущей функции ƒ, проходящей через точки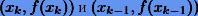 
.
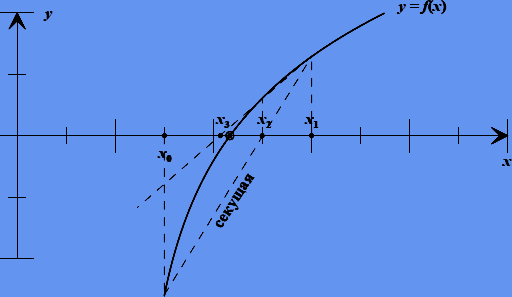
Рисунок 2.4 — Метод секущих
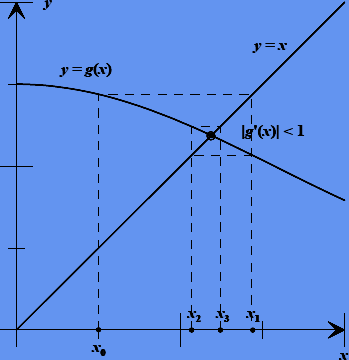
Рисунок 2.5 — Метод простых итераций