4.4 Метод Зейделя
Очевидно, что основной недостаток итерационных методов состоит в том, что для обеспечения их сходимости необходимо задавать достаточно точное начальное приближение. Однако в случае систем линейных уравнений имеют место такие условия, когда метод простых итераций в модификации Зейделя сходится всегда. В частности, известно, что метод Зейделя сходится, если система (4.2) нормальная. Согласно определению система (4.2) называется нормальной, если матрица A — симметричная и положительно определена.
Метод Зейделя обычно применяется к схеме простых итераций с диагональными элементами (4.15) матрицы H. В результате покомпонентное представление итерационной схемы принимает вид
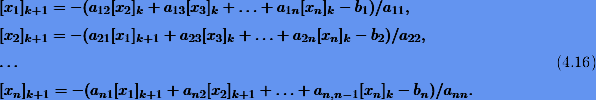
Примечательно, что любую систему линейных уравнений Ax = b можно привести к нормальному виду, если справа и слева ее домножить на транспонированную матрицу AT:

Такая процедура называется симметризацией Гаусса.
Таким образом, получение решения системы (4.2) методом Зейделя (4.16) теоретически возможно всегда, если применять его к эквивалентной нормальной системе (4.17). Правда, симметризация Гаусса может быть сопряжена со следующими трудностями: 1) скорость сходимости итерационного процесса для решения нормализованной системы может оказаться довольно низкой; и, кроме того, следует иметь в виду, что 2) симметризация ухудшает обусловленность системы.