ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

5.1 Степенной метод

Как известно, собственная пара 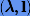, собственное число и соответствующий собственный вектор, удовлетворяют уравнению

Пусть матрица A имеет полную систему собственных пар , причем будем полагать, что . Заметим, что поскольку матрица A симметрична и положительно определена, ее собственные значения положительные, а собственные вектора ортогональны.

Рассмотрим произвольный ненулевой вектор x₀ и представим его разложение по ортонормированному базису из собственных векторов:

Без ограничения общности можно считать, что , поскольку в противном случае можно взять другой вектор x₀.

Последовательно умножая слева матрицу A на x₀, получаем итерационную схему

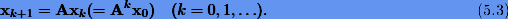
Согласно (5.1) и (5.2)

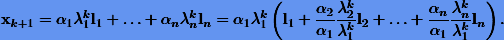
Отсюда видно, что с увеличением k в скобках будет доминировать первое слагаемое. Это означает, что итерационная схема (5.3) при больших k будет давать хорошее приближение собственного вектора l₁ по направлению, т.е. с точностью до множителя 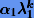. Для того чтобы схема (5.3) в пределе давала орту l₁, ее можно модифицировать как

После получения собственного вектора l₁ из формулы Рэлея для единичных векторов немедленно получаем соответствующее собственное число:

Далее будем искать собственный вектор l₂. Выберем произвольный вектор y, а в качестве начального вектора зададим

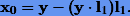
Нетрудно показать, что 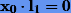, поэтому разложение вектора x₀ будет

Отсюда, применяя сначала схему (5.4), а затем (5.5), получим следующую собственную пару .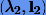

Таким образом, если найдены s — 1 собственных пар, то для поиска следующей пары 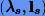используется сводка формул:

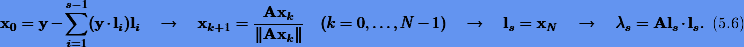
Здесь N — номер итерации, на которой достигается сходимость схемы (5.4) с некоторой точностью ε. Метод, определяемый формулами (5.6), называется степенным методом.

Следует иметь в виду, что вследствие накопления ошибок округления оценка собственного вектора x_k+1 может оказаться не ортогональной векторам 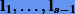. Для ее ортогонализации необходимо после каждой итерации в (5.6) вносить поправку к x_k+1

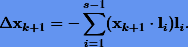
Кроме того, для определенности в алгоритме (5.6) в качестве произвольного вектора y можно взять любой из векторов ортонормированного базиса e_i, который бы давал ненулевой вектор x₀.

Интересно также заметить, что для получения последнего собственного вектора l_n в алгоритме (5.6) итерационный процесс (5.4) фактически не требуется, поскольку уже начальное приближение x₀ является собственным вектором, коллинеарным вектору l_n. Поэтому орта l_n может быть получена обычной нормировкой вектора x₀.