6 Решение задач оптимизации

Решение задач (безусловной) оптимизации в математической формулировке обычно сводится к минимизации некоторой функции Φ по ее переменным x: Φ(x) → min . Такая функция называется целевой. В свою очередь, минимум функции определяется из необходимого условия экстремума, т.е.

Следовательно, минимум функции является решением системы уравнений (6.1), для поиска которого можно использовать уже рассмотренные нами методы (раздел 3).

Для решения задачи минимизации наиболее часто применяются методы спуска, которые фактически являются аналогами метода простых итераций применительно к (6.1). Итерационная схема метода спуска имеет вид (3.8)

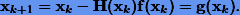
Как уже говорилось ранее, для сходимости этой схемы отображение 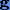должно быть сжимающее.

Если H представляет собой диагональную матрицу с равными диагональными элементами h, то получим схему градиентного спуска (рис. 6.1, а):

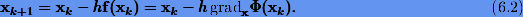
В схеме (6.2) коэффициент h неопределен. Если зададим h из условия

то получим так называемую схему наискорейшего градиентного спуска (рис. 6.1, б). Очевидно, метод наискорейшего градиентного спуска будет давать релаксационную последовательность приближений, в которой 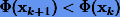для любых k. Если функция Φ представляет собой квадратичную форму с положительно определенной матрицей A:

то коэффициент h, соответствующий условию (6.3), будет

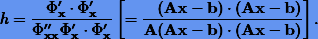
В соотвествии с записью (6.4) квадратичная форма имеет единственный минимум x=A^-1b. Очевидно, формулу для оптимального коэффициента h можно также использовать, когда минимизируемая функция Φ близка к квадратичной форме (6.4).

Для повышения скорости сходимости итерационного процесса можно использовать схему Ньютона

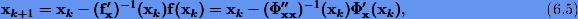
где 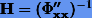так называемая матрица Гессе.

Нетрудно видеть, что при минимизации квадратичной формы (6.4) схема метода Ньютона будет давать точное решение уже на первой итерации (рис. 6.1, г). Действительно, это следует из того, что метод Ньютона фактически применяется к решению системы линейных уравнений Ax = b и в этом случае схема метода, как было показано в подразделе 4.3, вырождается в точное представление решения системы. Разумеется, применение метода Ньютона будет весьма эффективным при минимизации любой функции, близкой к квадратичной форме типа (6.4).

Следует заметить, что метод Ньютона обычно имеет малую область сходимости и для ее увеличения часто прибегают к так называемому методу ньютоновских направлений, схема которого получается из (6.5) путем домножения поправки на уменьшающий коэффициент h < 1:

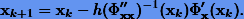
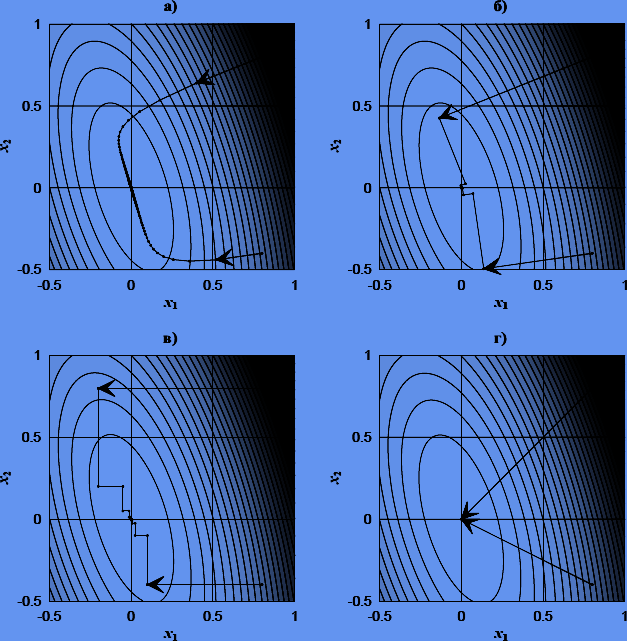
Рисунок 6.1 — Сходимость методов спуска при минимизации функции с начальными приближениями (0.8, 0.8) и (0.8, —0.4): а) метод градиентного спуска с h = 0.2; б) метод наискорейшего градиентного спуска; в) метод покоординатного спуска; г) метод Ньютона (стрелками указана первая итерация)

Довольно эффективным для решения задачи оптимизации может быть применение метода покоординатного спуска (рис. 6.1, в), который по сути является аналогом метода Зейделя. Метод просто состоит в поочередном поиске минимумов функции относительно одной переменной, что приводит к итерационному процессу последовательного решения скалярных уравнений

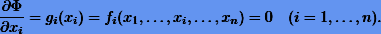
Здесь в каждом i-м уравнении все переменные, кроме искомой x_i, принимают значения, полученные на предыдущих этапах уточнения.