7.3.2 Полином Ньютона

Теперь рассмотрим полином g (7.3) степени n — 1.Тогда разделенная разность первого порядка

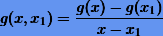
будет представлять собой полином степени n — 2, а разделенная разность второго порядка

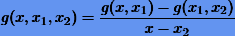
— полином степени n — 3; и так далее. Отсюда следует, что разделенная разность n-го порядка будет тождественно равна нулю.

Далее, из определения разделенных разностей получим

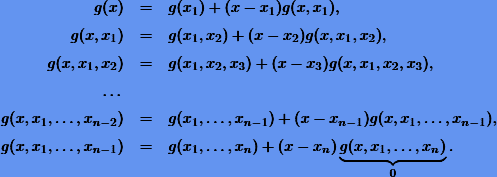
Осуществляя обратные подстановки и учитывая условие интерполяции (7.1), получим в итоге интерполирующий полином Ньютона:

Разделенные разности находятся из треугольника (7.7), хотя их можно вычислять иначе.

Введем обозначение 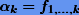и перепишем полином (7.8) в виде

Подставляя в (7.9) узловые значения, получаем

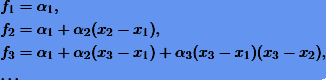
Отсюда будем иметь рекуррентные формулы для α:

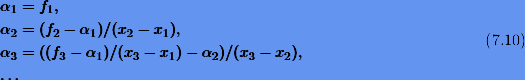
Используя дополнительные вспомогательные переменные, их можно переписать в компактном и более удобном для программировании виде:

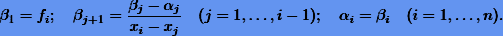
В то же время для вычисления значений полинома Ньютона1 в произвольных точках x следует прибегать к рекуррентной схеме Горнера:

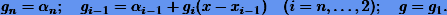
1Впрочем, как и любого полинома, записанного в канонической форме (7.3).