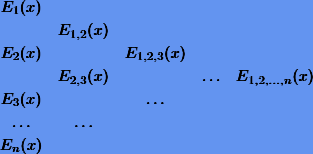7.4 Интерполяция Эйткена-Невилла
Для упрощения вычислений интерполяционного многочлена также удобно использовать так называемую схему Эйткена-Невилла.
Пусть 
— интерполяционный многочлен порядка k с узлами интерполяции 
для функции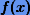 
, в частности, 
. Тогда справедливы равенства
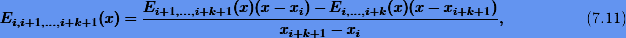
где 
— интерполяционный многочлен уже порядка k + 1 на сетке 
.
Докажем справедливость этой формулы по индукции. Пусть k = 0. Тогда будем иметь формулу
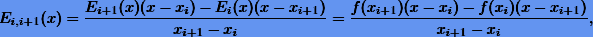
что представляет линейную интерполяцию по двум точкам.
Теперь допустим, что формула Эйткена-Невилла (7.11) верна для некоторого k = n — 1. Тогда для k = n формула перепишется как
где 
— интерполяционные многочлены степени n на сетках 
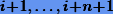и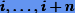 
соответственно, полученные по формуле (7.11), которая верна для получения всех интерполяционных многочленов до степени n. Следовательно, результирующий полином 
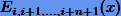будет иметь степень n + 1. Покажем, что он будет интерполирующим на сетке 
, т.е. для него в соответствующих узлах выполняется условие Лагранжа (7.1). Для крайних узлов xi и xi+n+1, очевидно,
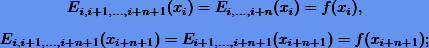
тогда как для всех внутренних узлов 
Таким образом, справедливость формулы Эйткена-Невилла (7.11) доказана.
Фактически, вычисление многочлена 
на сетке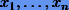 
сводится к последовательному вычислению с помощью (7.11) элементов таблицы
