7.5 Сходимость полиномиальной интерполяции
Возникает вопрос, будет ли стремиться к нулю погрешность интерполяции R(x) для любого x на заданном отрезке интерполяции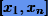 
при увеличении числа узлов n. Ответ, вообще говоря, отрицательный.
Дадим определение сходимости интерполяционного процесса. Говорят, что интерполяционный процесс сходится в точке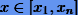 
, если
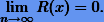
Сформулируем еще одно определение, связанное со сходимостью интерполяции. Интерполяционный процесс сходится равномерно на отрезке 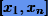для заданной последовательности узлов, если
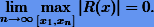
Понятно, что свойство сходимости процесса интерполяции зависит как от выбора последовательности сеток, так и от гладкости интерполируемой функции. По поводу сходимости есть две теоремы. В теореме Фабера утверждается, что какова бы ни была последовательность сеток, найдется такая интерполируемая функция, для которой интерполяционный многочлен не сходится равномерно на заданном отрезке интерполяции. С другой стороны, в теореме Марцинкевича говорится, что если интерполируемая функция непрерывна на отрезке интерполяции, то найдется такая последовательность сеток, для которых процесс интерполяции сходится равномерно. Например, для улучшения свойства сходимости интерполяционного процесса можно воспользоваться такими сетками, где в качестве узловых значений выбираются корни полиномов Чебышева.