7.7 Сплайн-интерполяция

Для разрешения проблемы сходимости процесса интерполяции часто прибегают к так называемой кусочно-полиномиальной интерполяции, когда отрезок 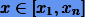делится на подотрезки, на каждом из которых выполняется полиномиальная интерполяция невысокой степени. Простой пример кусочно-полиномиальной интерполяции — это ломаная, для которой условия интерполяции (Лагранжа) выполняются в точках излома.

Одним из способов кусочно-полиномиальной интерполяции является интерполирование с помощью сплайн-функций. В чертежном деле сплайн — это гибкая линейка из дерева или пластика, предназначенная для проведения гладких кривых через заданные точки плоскости.

В вычислительной практике наиболее распространены кубические сплайн-функции, определяемые многочленами третьей степени. Обязательным условием интерполяционной кубической сплайн-функции является то, что она, а также ее первая и вторая производные являются непрерывными.

На каждой из подотрезков 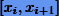кубический сплайн gi(x)определяется как

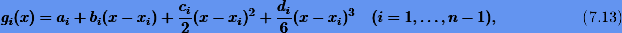
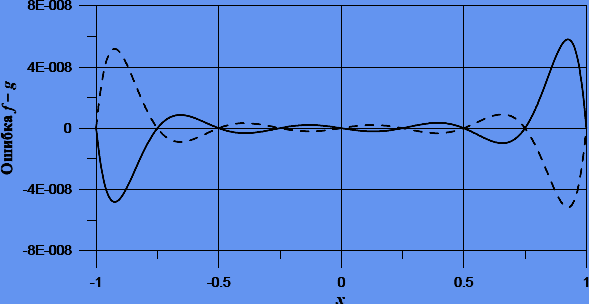
где ai, bi, ci и di — коэффициенты сплайна, подлежащие определению. Заметим, что

Рисунок 7.1 — Ошибка полиномиальной интерполяции для равномерного разбиения 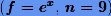. Пунктиром показана функция .

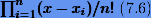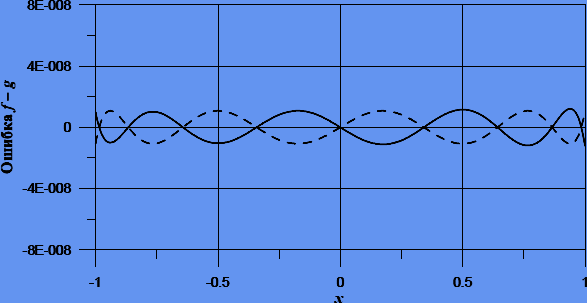
Рисунок 7.2 — То же, что и на рис. 4.1, но для неравномерного разбиения с узлами Чебышева.

Из условия Лагранжа (7.1) 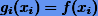. Кроме того, доопределим 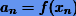. Тогда

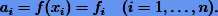
Далее, требование непрерывности сплайн-функции приводит к условиям 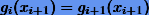или

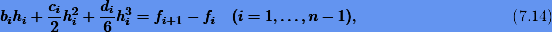
где 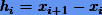. В свою очередь, условия непрерывности первой и второй производных 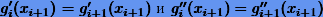дают

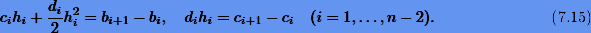
Таким образом, условия непрерывности дают 3(n — 1) — 2 уравнений для 3(n — 1) переменных bi, ci и di. Два недостающих уравнения обычно получают из граничных условий

Заметим, что второе соотношение получается из второй группы уравнений (7.15) при i = n — 1, если положить cn = 0.

Исключим теперь из уравнений (7.14) и (7.15) переменные bi и di. Для этого выразим из (7.14) разность bi+1 — bi и подставим ее в (7.15). Тогда будем иметь

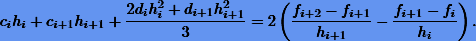
Используя вторую группу уравнений (7.15), исключим переменные di. В итоге получим систему ли¬нейных уравнений относительно неизвестных :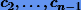

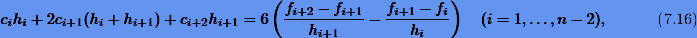
где 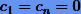. После нахождения из системы коэффициентов ci вычисляются сначала коэффициенты di, а потом bi:

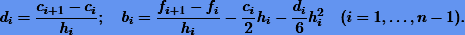
Перепишем систему (7.16) в матричном виде

где , H — квадратная матрица размера

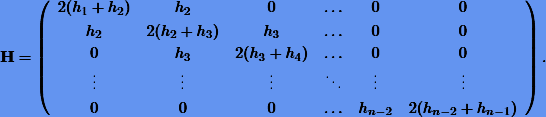
Для решения такой системы линейных уравнений применяется метод Гаусса, адаптированный к системам с трехдиагональной матрицей.

После прямого хода метода Гаусса матрица H и вектор Δ преобразуются к виду

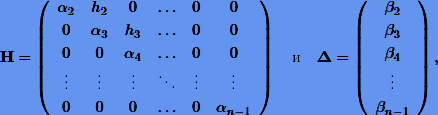
где

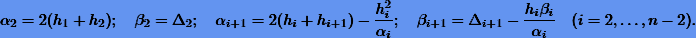
Наконец, обратный ход дает решение системы

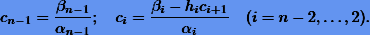
Итак, вычислив коэффициенты кубического сплайна, определяем затем, в какой подотрезок попадает значение x, и находим значение соответствующей интерполирующей кубической функции (7.13).