8 Метод наименьших квадратов
На практике к интерполяции обычно прибегают, когда измеренные значения зависимости ƒ имеют пренебрежимо малые погрешности. При достаточно больших погрешностях использование интерполяции не имеет смысла, поскольку уже условие (7.1) оказывается не обоснованным. В этом случае для построения аппроксимирующей функции g обращаются к методу наименьших квадратов.
Пусть аппроксимирующая функция g имеет m параметров 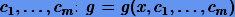 , причем
, причем  , где, как и ранее, n — число измерений. Идея метода наименьших квадратов состоит в том, чтобы среди всевозможных параметров
, где, как и ранее, n — число измерений. Идея метода наименьших квадратов состоит в том, чтобы среди всевозможных параметров 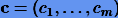 найти такие, при которых бы функционал
найти такие, при которых бы функционал

(сумма квадратов невязок g — f) принимал наименьшее значение: 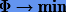 .
.