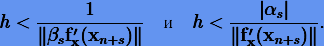
5.3. Предиктор-корректор

Неявная схема интегрирования предполагает итерационное решение системы нелинейных уравнений относительно искомого решения x_n+s. Для этого обычно применяют метод простых итераций. Легко показать, что в случае методов Адамса (5.4) и дифференцирования (5.7) итерации будут сходиться, если соответственно

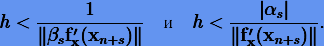
Итерационный процесс требует начального приближения решения нелинейной системы. Обычно его получают из явной схемы с точностью на порядок ниже. Явную схему называют предиктором, тогда как неявную — корректором, а итерационную процедуру в целом — предиктором-корректором. Например, для метода трапеций (неявного метода Адамса второго порядка) в качестве предиктора используют метод Эйлера (явный метод Адамса первого порядка), и тогда процедура предиктор-корректор (P−С) будет

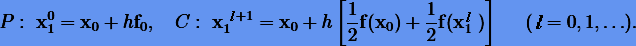
Интересно, что первый шаг итерационной последовательности дает решение метода Хойна.