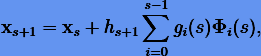
5.9. Выбор шага

Изменение величины шага для эффективного численного интегрирования в многошаговых методах гораздо сложнее, чем в одношаговых. Это связано с тем, что при использовании многошаговой схемы интегрирования получение каждого следующего решения на новом шаге предполагает перевычисление предыдущих решений на новой равномерной сетке с соответствующим шагом. Для этого, как правило, прибегают к интерполяционным многочленам. Главный недостаток такого подхода состоит в том, что вместе с решениями необходимо перевычислять и значения правых частей уравнений. Другой подход — это построение многошаговых схем интегрирования на неравномерной сетке.

Например, для (s + 1)-го решения при известных s предыдущих решениях обобщение явного метода Адамса на случай переменного шага дает формулу

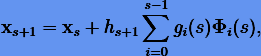
где

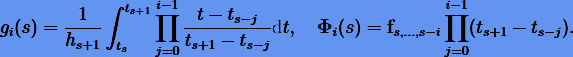
Для функций 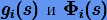возможно получить рекуррентные формулы. Тем не менее их перевычисление на каждом шаге чрезвычайно усложняет вычислительный процесс, и это является существенным недостатком в использовании многошаговых методов с переменным шагом.

Каждый следующий шаг интегрирования определяется, как и в одношаговых методах, по формуле (3.30), где в качестве 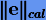можно использовать оценку (5.20).