6.3. Проекционный метод
Для сохранения интегралов систем дифференциальных уравнений часто применяют так называемый проекционный метод, который, по-видимому, впервые предложил П. Накози в 1971 г. Заметим, что исследуемая нами ранее система (6.5) вместе с интегральным соотношением (6.6) является частным случаем дифференциально-алгебраических систем уравнений, которые имеют вид
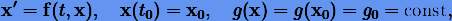
где в качестве алгебраического уравнения обычно выступают интегралы системы дифференциальных уравнений либо налагаемые на нее связи. Рассмотрим проекционный метод на примере этой системы.
Идея метода состоит в том, чтобы после каждой стандартной процедуры интегрирования на шаге вносить в численное решение 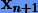 поправки
поправки 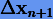 за отклонение
за отклонение 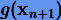 относительно
относительно 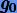 , т.е. чтобы
, т.е. чтобы
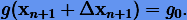
С точностью до малых первого порядка имеем
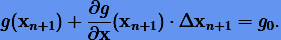 |
(6.12) |
Чтобы обеспечить наименьшую величину поправки 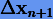 в соответствии с (6.12), ее направляют вдоль нормали к поверхности g(x) в точке
в соответствии с (6.12), ее направляют вдоль нормали к поверхности g(x) в точке 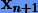 , представляя, таким образом, в виде
, представляя, таким образом, в виде
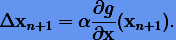 |
(6.13) |
Коэффициент α определяется после подстановки (6.13) в (6.12). В итоге будем иметь поправку
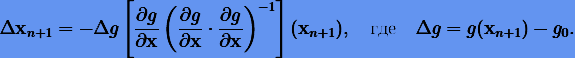 |
(6.14) |
Поскольку (6.14) получается из приближенного соотношения (6.12), то исправленное решение может еще не удовлетворять алгебраическому уравнению. В этом случае следует повторять процедуру уточнения решения (6.14) до тех пор, пока поправка 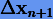 не станет достаточно малой.
не станет достаточно малой.
Интересно заметить, что если мы выполним в (6.10) приближенную замену
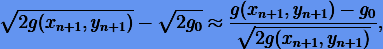
то получим коррекцию проекционного метода (6.14) применительно к дифференциально-алгебраической системе гармонического осциллятора (6.5) и (6.6).