6.2. Методы Эйлера
Применим теперь к уравнениям (6.5) явный и неявный методы Эйлера:
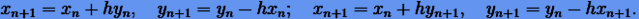 |
(6.7) |
Разрешение в неявной схеме (n + 1)-го решения относительно n-го решения дает
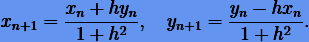
Отсюда видно, что результаты интегрирования, получаемые методами Эйлера на одном шаге, совпадают с точностью до коэффициента 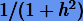 . Подставляя решения в интегральное соотношение g(x, y) (6.6), получаем для явного метода
. Подставляя решения в интегральное соотношение g(x, y) (6.6), получаем для явного метода
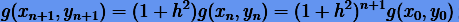
и для неявного
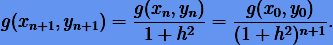
Как видно, при пошаговом интегрировании методами Эйлера интегральное соотношение не сохраняется: в явном случае оно увеличивается, тогда как в неявном уменьшается.
Далее поскольку преобразование сдвига по времени (6.2) симплектично, то пошаговое отображение в соответствии со схемой интегрирования
 |
(6.8) |
также должно быть симплектическим.
Проверим на симплектичность схемы Эйлера. Вычислим скобки Пуассона
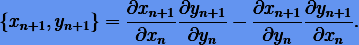 |
(6.9) |
Тогда для явного и неявного методов соответственно получаем 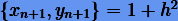 и
и 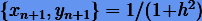 . Вместе с тем известно, что преобразование (6.8) симплектично, если скобка Пуассона равна единице. Следовательно, методы Эйлера не симплектичны.
. Вместе с тем известно, что преобразование (6.8) симплектично, если скобка Пуассона равна единице. Следовательно, методы Эйлера не симплектичны.
Обратимость по времени (6.3) уравнений (6.5) требует, чтобы схема интегрирования при ее последовательном использовании сначала с шагом h, а затем с шагом — h давала исходные результаты. Однако согласно схемам Эйлера (6.7) будем иметь:
в явном случае

в неявном случае
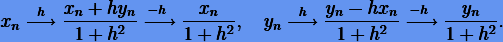
Следовательно, схемы Эйлера не обратимы по времени.
Таким образом, методы Эйлера не геометрические. Хотя они могут стать таковыми после введения ряда незначительных модификаций.
Простым способом сохранения интегрального соотношения (6.6) является возвращение численного решения каждого шага на интегральную кривую, задаваемую уравнением 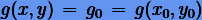 . Как видно из (6.6), интегральные кривые уравнений гармонического осциллятора представляют собой концентрические окружности с центром в начале координат и радиусами
. Как видно из (6.6), интегральные кривые уравнений гармонического осциллятора представляют собой концентрические окружности с центром в начале координат и радиусами 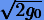 определяемыми начальными условиями. Перемещения численных решений
определяемыми начальными условиями. Перемещения численных решений 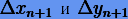 будем осуществлять вдоль нормали к интегральной кривой в точке
будем осуществлять вдоль нормали к интегральной кривой в точке 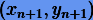 , т.е. вдоль вектора положения этой точки в фазовом пространстве. Тогда из геометрических соображений нетрудно получить поправки к решениям
, т.е. вдоль вектора положения этой точки в фазовом пространстве. Тогда из геометрических соображений нетрудно получить поправки к решениям
 |
(6.10) |
Интересно, что простой формальной заменой в схемах (6.7) первых (или вторых) частей для приближенных решений 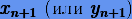 удается получить две явные симплектические схемы интегрирования
удается получить две явные симплектические схемы интегрирования
 |
(6.11) |
Симплектичность модифицированных методов Эйлера несложно проверить, вычислив, как и ранее, скобки Пуассона (6.9), которые оказываются равными единице в обоих случаях.
Комбинируя схемы интегрирования методов Эйлера, можно получить новую, удовлетворяющую условию обратимости по времени (6.3): применим сначала явную схему Эйлера с шагом h/2, а затем — неявную с тем же шагом, в итоге будем иметь схему метода трапеций
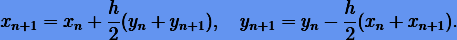
Поскольку метод трапеций симметричен, он будет удовлетворять условию обратимости (6.3).