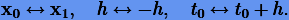
6.4.2. Простые симметрические методы

Как мы уже отмечали, условию обратимости (6.3) отвечают симметрические методы. Для их построения часто прибегают к комбинированию обычных методов Рунге − Кутты с их смежными методами.

Смежным к исходному методу Рунге − Кутты (3.33) называется метод, получаемый в результате замены в исходном методе

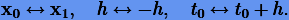(6.16)

Очевидно, повторная замена дает исходный метод, иначе говоря, смежный к смежному методу является исходным.

Смежный метод также является методом Рунге − Кутты, коэффициенты которого 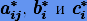связаны коэффициентами исходного метода 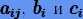как

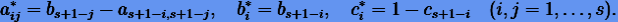(6.17)

Действительно, выполнив замену (6.16) в методе (3.33), приводим его к смежному виду

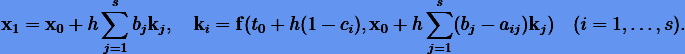
Чтобы упорядочить в формуле 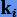по возрастанию коэффициентов 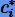, нам остается произвести замену индексов 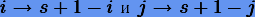. В итоге находим связь между коэффициентами (6.17).

Если исходный метод имеет порядок p, то ввиду замены (6.16) смежный метод будет аппроксимировать решение x(t₀) в окрестности с ошибкой порядка 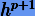, следовательно, и смежный метод будет иметь порядок p.

Нетрудно видеть, что смежный к явному методу Эйлера будет неявный и наоборот. Интересно, что и симплектические методы Эйлера (6.15) также взаимосмежные. В то же время метод средней точки

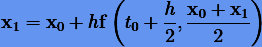
и метод трапеции

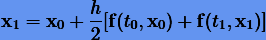
остаются без изменения относительно преобразований (6.16). Такие методы, как мы уже говорили (разд. 4.3), называются симметричными.

Введение смежных методов позволяет путем комбинирования их с исходными очень просто конструировать симметрические методы. Пусть 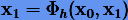— исходная схема интегрирования на шаге h, a 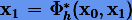— смежная. Тогда последовательное использование на половине шага сначала смежного метода, а затем исходного 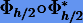или наоборот 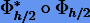дает симметричный метод. Симметричность следует из того, что 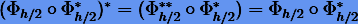. То же самое справедливо и для второго случая. Например, если мы применим на полшага сначала явный метод Эйлера, а затем неявный, то получим метод трапеций; если в обратном порядке — метод средней точки. Следует заметить, что результирующие методы имеют уже второй порядок, тогда как их составляющие — первый.