3.8. Порядок и шаг интегрирования при компьютерной реализации метода
Теоретически совместное увеличение порядка и уменьшение шага метода неограниченно повышает методическую точность численных результатов интегрирования. Однако при компьютерной реализации в арифметике с определенной точностью вследствие ошибок округления существуют такие значения параметров интегрирования, которые дают предельно высокую методическую точность ввиду того, что методические ошибки становятся соизмеримыми с ошибками округления, и в этом случае не имеет смысла предпринимать какие-либо дальнейшие попытки получить более высокую точность численного интегрирования.
Получим оценки оптимальной пары порядок-шаг интегрирования применительно к численному решению дифференциальных уравнений круговой двумерной задачи двух тел:
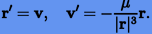
Здесь 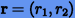 и
и 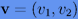 — векторы положения и скорости соответственно,
а
— векторы положения и скорости соответственно,
а 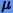 — гравитационный параметр. Поскольку
— гравитационный параметр. Поскольку 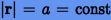 , будем полагать, что
величина
, будем полагать, что
величина 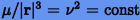 , т.е. решение
, т.е. решение 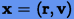 описывается уравнениями гармонического осциллятора с частотой
описывается уравнениями гармонического осциллятора с частотой 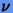 и может быть записано в виде
и может быть записано в виде
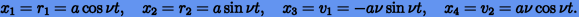 |
(*) |
Оценим методическую ошибку  по главному члену погрешности 2.5:
по главному члену погрешности 2.5:
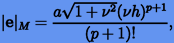 |
(*) |
где использована формула 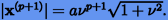 .
Согласно формулам методов Рунге − Кутты ошибку округления
.
Согласно формулам методов Рунге − Кутты ошибку округления 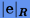 можно оценить как
можно оценить как
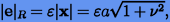 |
(**) |
где  — машинное эпсилон.
— машинное эпсилон.
Очевидно, что не имеет смысла выбирать такие шаг и порядок интегрирования, при которых методическая
ошибка будет меньше ошибки округления. Из условия 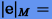
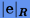 получим отношение
между оптимальными параметрами интегрирования
получим отношение
между оптимальными параметрами интегрирования 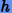 и
и 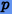
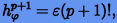 |
(***) |
где 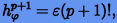 — шаг по долготе
— шаг по долготе  , соответствующий шагу
, соответствующий шагу 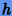 .
.
Отношение (***) дает нижнюю границу для шага 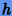 , в то время как для неявных методов имеет место верхняя
граница, задаваемая условием (3.38). Если положить, что
, в то время как для неявных методов имеет место верхняя
граница, задаваемая условием (3.38). Если положить, что 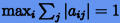 (в действительности максимум
близок к единице), то получим следующее ограничение на шаг интегрирования
(в действительности максимум
близок к единице), то получим следующее ограничение на шаг интегрирования 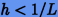 или
или 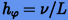 .
Оценим постоянную Липшица
.
Оценим постоянную Липшица 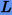 для исследуемой задачи.
для исследуемой задачи.
Рассмотрим отношение
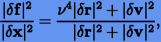
где 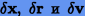 — всевозможные разности векторов в соответсвующих переменных.
Принимая
— всевозможные разности векторов в соответсвующих переменных.
Принимая 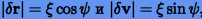 , где
, где 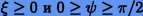 , будем иметь
, будем иметь
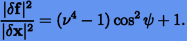
Отсюда нетрудно видеть, что все значения отношения лежат между 1 и 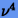 .
Следовательно, согласно (1.9) в качестве постоянной Липшица можно выбрать
.
Следовательно, согласно (1.9) в качестве постоянной Липшица можно выбрать
 . Тогда получаем верхнюю границу шага
. Тогда получаем верхнюю границу шага
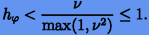
Таким образом, в лучшем случае, а именно при  , когда верхняя граница максимальна,
шаг интегрирования
, когда верхняя граница максимальна,
шаг интегрирования 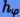 должен удовлетворять неравенствам
должен удовлетворять неравенствам
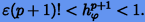
Очевидно, условие
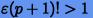
означает, что порядок метода завышен и использование такого метода при вычислениях
в арифметике с точностью  не разумно в том смысле, что ту же точность
результатов интегрирования можно получить с использованием методов более низких порядков.
Оптимальные порядки
не разумно в том смысле, что ту же точность
результатов интегрирования можно получить с использованием методов более низких порядков.
Оптимальные порядки 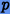 неявных методов Рунге − Кутты для различных
неявных методов Рунге − Кутты для различных  , соответствующих
одинарной, двойной, расширенной и четверной точности, представлены в таблице.
Хотя следует иметь в виду, что эти порядки получены для задачи с
, соответствующих
одинарной, двойной, расширенной и четверной точности, представлены в таблице.
Хотя следует иметь в виду, что эти порядки получены для задачи с  . В ином случае
они могут быть меньше.
. В ином случае
они могут быть меньше.
Максимально приемлемые порядки 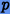 неявных методов для различных
неявных методов для различных 
