6.4.5. Особенности в использовании симплектических методов

Очевидно, вдоль точного решения канонической системы ее гамильтониан сохраняется, тогда как вдоль приближенного решения нет. Тем не менее в силу симплектичности схем интегрирования они будут сохранять другой, близкий к оригинальному гамильтониан. Так, нетрудно убедиться, что методы Эйлера (6.11) не сохраняют интеграл гармонического осциллятора (6.6), однако их приближенные решения на каждом шаге удовлетворяют другим интегральным соотношениям

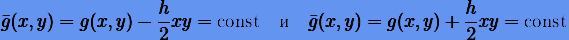(6.25)

соответственно для первой и второй схем (6.11). Функции 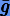еще называют связанными гамильтонианами. Соотношения (6.25) описывают эллипсы, большие полуоси которых направлены вдоль прямых y = x и y = −x. Таким образом, приближенные решения 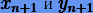(6.11) согласно (6.25) будут лежать на замкнутых и компактных (при малых h) кривых, поэтому ошибка в g будет ограничена:

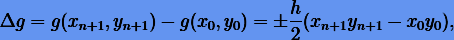
хотя при использовании обычных (негеометрических) методов ее величина имеет тенденцию к неограниченному росту.

В случае применения методов Эйлера (6.15) для интегрирования канонической системы с произвольным гамильтонианом g известно, что связанный гамильтониан будет иметь вид

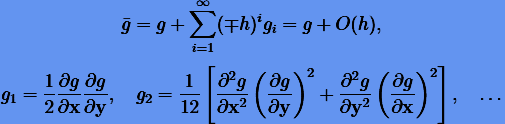(6.26)

В степенном ряде (6.26) знак минус при h соответствует первой схеме Эйлера (6.15), тогда как плюс — второй. Если используются симплектические методы p-го порядка, то связанный гамильтониан формально можно представить как

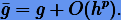
Таким образом, симплектический метод будет сохранять связанный гамильтониан 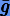, близкий к оригинальному g, причем близость гамильтонианов определяется не только величиной шага интегрирования h, но и порядком метода p. Это, в свою очередь, обеспечивает ограниченность ошибки Δg.

Следует заметить, что интегральное соотношение 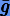= const явно зависит от h, поэтому оно будет сохраняться только при постоянном шаге. Если шаг переменный, то связанный гамильтониан уже не будет интегралом, и в этом случае ограниченность ошибки Δg не гарантируется. Так, при симплектическом интегрировании орбиты задачи двух тел с переменным шагом гамильтониан задачи (кеплеровская энергия) не сохраняется и ошибка в интегральном соотношении неограниченно возрастает. В связи с этим для эффективного использования симплектических методов необходимо выполнять интегрирование с постоянным шагом.

Впечатляющими оказываются результаты при использовании симплектической схемы средней точки, которая также является симметрической. Применительно к уравнениям гармонического осциллятора она точно сохраняет гамильтониан системы. Следует заметить, что в случае линейных систем дифференциальных уравнений схема средней точки совпадает с симметричной схемой трапеций, которая, вообще говоря, не симплектична. Вместе с тем во многих последних работах по геометрическим интеграторам показывается, что симметрические методы так же, как и симплектические, позволяют ограничить ошибки в гамильтониане при интегрировании канонических систем.