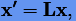
3.12. А-устойчивость методов Рунге − Кутты

Свойства устойчивости численных методов интегрирования обычно исследуют на примере асимптотически устойчивых систем линейных уравнений

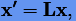(3.63)

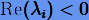где L — квадратная матрица размера m × m с постоянными коэффициентами, собственные числа которой имеют отрицательные действительные части: . Введем преобразование координат

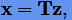(3.64)

которое приводит матрицу L к жордановой канонической форме:

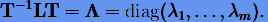(3.65)

Тогда в новых переменных z система (3.62) преобразуется к виду

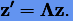(3.66)

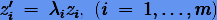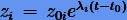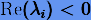Поскольку Λ — диагональная матрица, то система (3.65) расщепляется на m независимых уравнений , которые соответственно имеют решения , где компоненты начального вектора z₀ определяются по x₀ согласно линейному преобразованию (3.63): . Ввиду того, что для всех i, следовательно, z → 0 при t → ∞, следовательно и x → 0. Естественно, для качественного описания решения системы (3.62) численным методом необходимо потребовать, чтобы

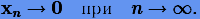(3.67)

Метод, обеспечивающий выполнение (3.66), называется устойчивым. Поскольку все методы Рунге − Кутты сходящиеся, теоретически всегда можно подобрать такой достаточно малый шаг интегрирования, при котором будет выполняться условие (3.66). В связи с этим представляет интерес определение максимально допустимого шага h, когда условие (3.66) будет нарушаться. Если условие (3.66) выполняется для любого h, говорят, что численный метод абсолютно устойчив либо А-устойчив.

Покажем теперь, что между численными решениями систем (3.62) и (3.65), полученными методом (3.33), имеет место линейное соответствие, т.е. 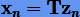. Для систем линейных уравнений схемы интегрирования на шаге h согласно (3.33) можно записать в виде

где 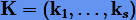для системы (3.62), а 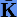— соответствующая матрица коэффициентов для системы (3.65); 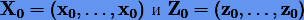— матрицы размера m × s, тогда как

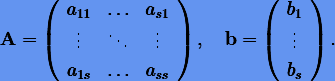
Рекуррентные формулы для 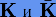в (3.67) дают

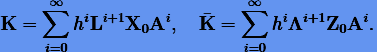(3.68)

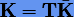Отсюда, используя связь между матрицами L и Λ (3.64) и соотношение , можно показать, что , поэтому согласно представлению решений 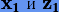(3.67) . Тогда очевидно, что линейное соответствие будет иметь место и для других решений 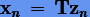. Следовательно, условие (3.66) будет выполняться, если при 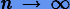и, таким образом, устойчивость численного метода можно исследовать на примере более простой системы (3.65) с независимыми друг от друга уравнениями. Поскольку эти уравнения однотипны, исследование устойчивости фактически сводится к рассмотрению одного уравнения общего вида

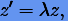(3.69)

где 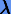— комплексное число, причем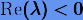

Исследуем на предмет устойчивости некоторые простейшие методы Рунге − Кутты, а именно: явный (2.7) и неявный (3.34) методы Эйлера (p = 1), а также метод Хойна (3.13) и трапеций (3.35) (р = 2). Схемы интегрирования методов применительно к уравнению (3.69) можно представить в виде — так называемые функции устойчивости, которые в порядке перечисления методов представимы как

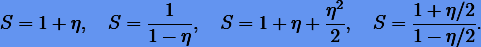
Очевидно, метод будет устойчивым при заданной паре чисел h, и λ, если .

На рис. 3.2 показаны области устойчивости методов 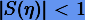(серая заливка) на комплексной плоскости 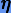. Поскольку 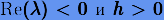, то нас интересует левая полуплоскость 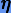. Из рисунка видно, что рассматриваемые явные методы имеют ограниченные области устойчивости, что говорит об ограничении в выборе величины шага интегрирования h с точки зрения качественного описания решения. Напротив, неявные методы не имеют никаких ограничений на шаг h, поскольку левая полуплоскость 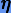оказывается в области устойчивости методов. Следовательно, рассматриваемые неявные методы абсолютно устойчивы.

Заметим, что из численного анализа известно, что среди явных методов нет абсолютно устойчивых. Это главным образом обусловлено тем, что функция устойчивости для любого явного метода представляет собой полином вида , величина которого неограниченно возрастает при .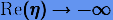

В то же время среди неявных методов имеется немало А-устойчивых, которые образуют класс основных методов, используемых для получения приближенных решений так называемых жестких систем. Напомним, что система линейных дифференциальных уравнений типа (3.62) называется жесткой, если она плохо обусловлена, т.е. если отношение 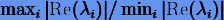достаточно большое.

Рис. 3.2. Области устойчивости методов Рунге − Кутты низких порядков: а — метод Эйлера;
б — неявный метод Эйлера; в — метод Хойна; г — метод трапеций